江苏农信社考试财务管理（2）
第二章  财务管理基础观念
第一节  资金时间价值
    资金时间价值的计算
    (一) 单利的计算
    单利是只对本金计算利息，而不将以前计息期的利息累加到本金中去，即利息不再生息。在单利计算中，经常使用以下符号：
    p--本金，又称期初金额或现值；i--利率，通常指每年利息与本金之比； I--利息；
    S--本金与利息之和，又称本利和或终值；
    t--时间，通常以年为单位。
    1．单利利息
    单利利息的计算公式为：
    I = p·i·t
    [例2—1] 某企业有一张带息期票，面额为1 200元，票面利率4％，出票日期6月15日，8月14日到期(共60天)，则到期时利息为：
    I = l 200×4%×（60/360) = 8（元）
    在计算利息时，除非特别指明，给出的利率是指年利率。对于不足一年的利息，以一年等于360天来折算。
    2．单利终值
    单利终值的计算公式为：
    s = p + p·i·t= p·(1 + i·t)
    假设例2—l带息期票到期，出票人应付的本利和即票据终值为：
    s = l 200×[1十4％×（60/360）] = 1 208（元）
    (二)复利的计算
    按照复利计算法，每经过一个计息期，要将所生利息加入本金再计利息，逐期滚算，俗称“利滚利”。这里所说的计息期，是指相邻两次计息的时间间隔，如年、月、日等。除非特别指明，计息期为—年。
    1．复利终值
    [例2—2] 某人将l0 000元投资于一项事业，年回报率为6％，经过一年时间的期终金额为：
    s = p + p·i= p·(1 + i)= 10 000×(1 + 6%)= 10 600(元)
    若此人并不提走现金，将10 600元继续投资于该事业，则第二年本利和为：
    s = [p·(1+i)]·(1+i) = P·(1+i)2 = 10 000×(1十6％)2 = 10 000×1.1236 = 11 236(元)
    同理，第三年的期终金额为：
    s = p·(1十i)3
      = 1OOOO×(1 + 6%)3
      = 10 000×l.19lO
      = 11 91O(元)
    第n年的期终金额为；
    s = p(1 + i)n
    上式是计算复利终值的一般公式，其中的(1 + i)n被称为复利终值系数或1元的复利终值，用符号(s／p，i，n)表示。例如，(s／p，6%，3)表示利率为6％，3期复利终值的系数。
    2．复利现值
    复利现值是复利终值的对称概念，指未来—定期间的特定资金按复利计算的现在价值，或者说是为取得将来一定本利和现在所需要的本金。
    复利现值计算，是指已知s、i、n时求p.
    通过复利终值计算已知：
    s = p·(1 + i)n
    所以： p = s/(1 + i)n = S·(1 + i)-n
上式中的(1 + i)-n 是把终值折算为现值的系数，称复利现值系数，或称l元的复利现值，用符号(p／s，i，n)来表示。例如，(p／s，10％，5)表示利率为10％时5期的复利现值系数。
    3．复利息
    本金p的n期复利息等于：
    I = s - p
    [例2—6] 本金1 000元，投资5年，利率8％，每年复利一次，其本利和与复利息是：
    s = 1 000×(1+8%)5  = 1 000×1.469 = 1 469（元）
    I = 1 469 - 1 000 = 469(元)
    4．名义利率与实际利率
    复利的计息期不一定总是一年，有可能是季度、月或日。当利息在一年内要复利几次时，给出的年利率叫做名义利率。
    [例2—7] 本金l 000元，投资5年，年利率8％，每季复利一次，则：
    每季度利率 = 8％÷4 = 2％
    复利次数 = 5×4 = 20
    s = 1 000×(1+2%)20= 1 000×1.486= 1 486（元）
    I = 1 486 - 1 000= 486（元）
    实际年利率和名义利率之间的关系是；
    1+i =(1 + )m   n
式中：r —— 名义利率；
          m —— 每年复利次数；
          i —— 实际利率。
    将例2—7数据代入：
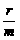
    i = (1+ )m - 1
      =（1+8%÷4)4 - l
      = 1.0824 - 1
      = 8.24%
    s = 1 000×（1 + 8.24%)5
      = 1 000×1.486
      = 1 486（元）