江苏农信社考试财务管理（4）
第二章  财务管理基础观念
第一节  资金时间价值
3．递延年金
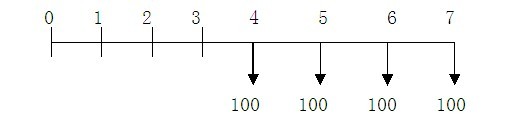
递延年金是指第一次支付发生在第二期或第二期以后的年金。递延年金的支付形式见图2—5。从图中可以看出，前3期没有发生支付，一般用m表示递延期数，本例的m＝3。第一次支付在第四期期末，连续支付4次，即n=4。
    m=3   i= 10%  n=4

递延年金的终值大小，与递延期无关，故计算方法和普通年金终值相同：
s = A•（s/A，i，n）
  = 100×(s／A，10％，4)
  = 100×4.641
  = 464.1（元）
    递延年金的现值计算的方法，是假设递延期中也进行支付，先求出(m+n)期的年金现值，然后，扣除实并未支付的递延期(m)的年金现值，即可得出最终结果。
    p（m+n） = 100×(p／A，i，m+n)
          = 100× (p／A，10％，3+4)
          = 100× 4.868
          = 486.8(元)
    p（m） = 100×(p／A，i，m)
         = 100× (p／A，10％，3)
         = 100× 2.487
         = 248.7(元)
    p（n） = P（m+n） -  P（m）
         = 486.8 - 248.7
         = 238.1(元)
    4．永续年金
    无限期定额支付的年金，称为永续年金。现实中的存本取息，可视为永续年金一例。
永续年金没有终止的时间，也就没有终值。永续年金的现值可以通过普通年金现值的计算公式导出：
    p = A •[1-(1+ i)-n]/i
    当n→∞时，(1+ i)-n 的极限为零，故上式可写成：
    p = A/i
    [例2—14] 拟建立一项永久性的奖学金，每年计划颁发10 000元奖金。若利率为l0％，现在应存入多少钱?
p = 10 000÷10% = 100 000（元）

更多江苏农信社考试、2014年江苏农村信用社招聘关注江苏银行招聘网